Motivation

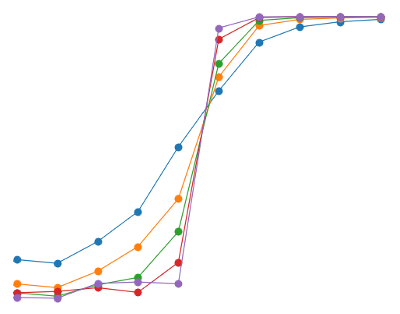
Magnetic systems offer themselves as the ideal benchmark for generic concepts pertaining to collective phenomena in nature. This is due in part to the availability of a large variety of diverse magnetic materials that can be chosen to approximate simple theoretical “toy models” of collective behavior and, in part, to their ease of study by a battery of experimental techniques.¹

The MARQOV project focuses on the development of an adaptable framework for the simulation and analysis of equilibrium lattice spin models and its optimization on massively parallel architectures. As this area of research, with origins in statistical physics, particularly aims at improving our understanding of critical phenomena ², there exists considerable overlap with other research fields, such as solid-state physics, material science, and high-energy physics. In general, phase transitions are characterized by the emergence of long-range collective behavior of the individual microscopic degrees of freedom. This gives rise to the important phenomenon of universality³, according to which the character of a phase transition is solely determined by only few fundamental properties of the system (such as its global symmetries and interaction ranges). Theoretically, the emergence of universality can be motivated by renormalization group approaches⁴, where at criticality the system forgets about its microscopic realization under repeated scale transformations.

Quenched spatial disorder, however, can present a relevant perturbation to the phase transition, leaving the character of the transition unchanged in some scenarios⁵⁶⁷, but leading to entirely different critical behavior in others⁸⁹¹⁰. Spatial disorder is not only of theoretical interest though, but in fact intrinsic to most real systems, arising from impurities, defects, and other inhomogeneities.

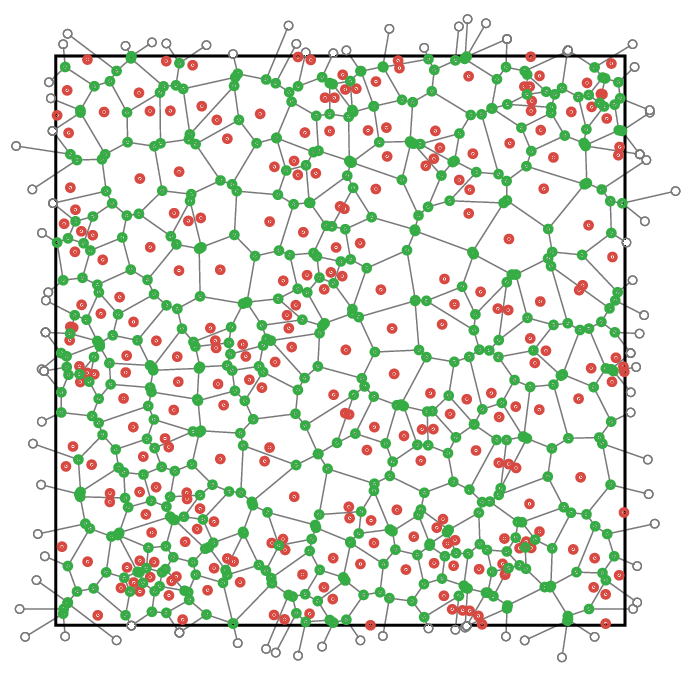
Figure 1. Voronoi graph generated from a random point cloud.

In principle, the role of uncorrelated randomness (such as in the form of diluted regular lattices) is successfully explained by Harris' seminal criterion¹¹, using a remarkably simple argument of competing fluctuation scales. The role of topological randomness, i.e., lattices with random connectivity (see Fig. 1 for an example), however, has yet to be fully understood. Recent contributions in this field¹²¹³ still strongly rely on numerical simulations, as topological disorder has so far not been within the reach of analytical methods. Specifically, the MARQOV code was recently used for probing disordered geometries and determine whether the universal character of an Ising transition is broken with respect to the clean model without disorder¹⁴¹⁵¹⁶. Finally, Ising-like systems are also studied on abstract topologies like scale-free¹⁷¹⁸ and small-world networks¹⁹²⁰ as well as in curved geometries such as the hyperbolic plane²¹, see Fig. 2.

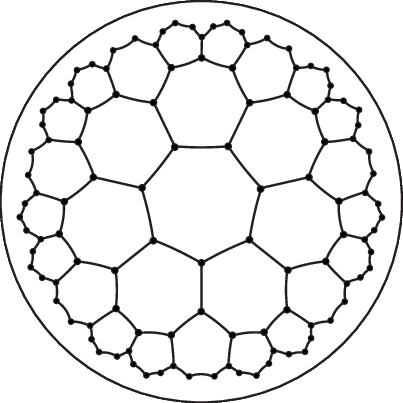
Figure 2. Regular heptagonal hyperbolic tessellation.

Apart from being used as a probe to investigate aspects of topology and disorder relevance, the Ising model, due to its conceptual simplicity, is widely applied in different areas of research. Besides uniaxial magnets, it describes, e.g., experimental liquid-vapor transitions and binary mixtures, certain transitions in high-energy physics (see [^13] and references therein), voter dynamics²² and can even be found in fairly unexpected applications such as the dynamics of traffic signals²³ or pistachio trees²⁴. Generalizing the Ising model to \( O(N) \) symmetric spin vectors, one obtains the XY model (\( N=2 \)), featuring a Kosterlitz–Thouless transition and the Heisenberg case (\( N=3 \)), which models certain real magnetic materials. Even higher symmetries (\(N=4,5\)) become, for instance, again relevant in particle physics and high-temperature superconductor transitions (see Ref. ²⁵ for a comprehensive review).

This large scope of applications justifies the continued relevance of classical spin models through decades of research. However, a comprehensive software package for those models does not exist to this date. Filling this gap, MARQOV offers a software framework combining modern HPC-optimized numerical simulation techniques and a state-of-the-art statistical analysis into a convenient workflow. Beyond that, MARQOV’s particular strengths include quenched disordered and frustrated systems, such as spin glasses, where parallelization and automatization aspects become important.